Under the hood

The physics of projectile ballistics

A projectile is initially accelerated (interior ballistics), passes through some intermediate space which may be filled with a fluid such as air (exterior ballistics), and then interacts with its target (terminal ballistics). This document will be concerned primarily with the target interaction and secondarily with the interactions with the fluid (if any) between the projectile accelerator and the target.

Very often, the quantity of primary interest is the penetration, or distance the projectile can move through the target before it will be brought to a stop. Penetration is nearly universally a function of sectional density, or mass divided by the frontal area, of the projectile. In most physically relevant situations, this is a strictly linear function (with one important exception, which will be discussed later). The penetration is also a function of the projectile speed. At relatively low speeds, penetration is nearly quadratic in speed, but as speed increases the penetration becomes only weakly speed dependent until, at the very highest speeds the penetration is essentially constant. The penetration is not always a monotonically increasing function of speed, in some circumstances there is a speed that gives maximum penetration and lower or higher speeds will result in decreased penetration.

We will discuss the penetration in various physical regimes.

Non-deforming projectiles

The simplest cases to analyze are where the projectile retains structural integrity as it penetrates its target.

Low speed penetration

At low speeds, the primary impediment to penetration is material strength. It takes a certain amount of pressure or tension (generalized as stress in the technical litterature) to deform a material by a given amount. For penetration, we are primarily concerned with the pressure exerted by the projectile on the target. If the pressure is below the elastic strength of the target, the target will not be permanently affected and will just bounce back into shape when the pressure is removed. Beyond the elastic limit, the target will suffer permanent deformations. If the pressure exceeds the yield strength, the target material begins to weaken as it deforms leading to a runaway deformation ultimately resulting in rupture. For thick targets, however, the projectile also needs to compress the material in front of it and to the sides to allow enough room for the projectile to pass. The pressure at which this compressive penetration can occur is called the cavity strength, which is usually about three times the yield strength.

Pressure P is a force F per area A
P = F / A.
The change in energy of a system dE is the force exerted on the system (in this case the projectile) times the distance over which the force is exerted dx
dE = -F dx
where the minus sign indicates the force is in the opposite direction of the projectile motion, so that its energy is being reduced. For penetration of a thick target to occur, we need the pressure to equal the cavity strength
P = Y_c.
Combining these relations, we find
dE = Y_c A dx.
Since this relation is linear, if we know the energy E of the projectile when it initially hits the target, we can easily find the distance penetrated x_p
x_p = E / (Y_c A).
For the purpose of this discussion, we can ignore the potential energy of the projectile, so that its energy is given by its kinetic energy alone
E = ½ m v²
where m is the projectile mass and v is its speed. We now have

xp =	m	v²	.
	A	2 Yc

As mentioned, in this regime penetration is linear in sectional density m/A, and quadratic in speed.

This is the realm of slings and arrows. Bullets are moving fast enough that other forces come into play.

High speed penetration

As a projectile pushes its way through the target, it must move the target material out of its way. This imparts kinetic energy to the target material that must come from the projectile, and the faster the projectile is going, the faster the target material must end up travelling in order to get out of the way in time and the move energy is used. At high enough speeds, these dynamic forces needed to push the target material out of the projectile path far exceed the material strength of the target and the physics of the problem becomes one of hydrodynamics - at these speeds, the target can be considered a fluid without material strength.

In this hydrodynamic regime, the projectile will experience a drag force equal to
F_d = ½c_d A v² ρ_t
where c_d is the coefficient of drag and ρ_t is the density of the material through which the projectile is moving. In a true fluid, where the fluid flows back around the end of the projectile, c_d can be significantly lower than 1 to perhaps 0.1 for long, thin darts. In targets that are rigid however, it is found that c_d ≈ 1.

Again, the change in the projectile energy is the force times the distance moved. Plugging in our expression for the force we have
dE = -½c_d A v² ρ_t dx.
Note, however, that the kinetic energy of the projectile is ½ m v², so that we may write
dE = -c_d A (E/m) ρ_t dx.
This is the differential equation for exponential decay, giving us
E(x) = E₀ exp(-c_d (A/m) ρ_t x).
We see that there is a characteristic length x_c = (m/A) × 1/(c_d ρ_t) after which the projectile kinetic energy will have dropped to a factor of 1/e ≈ 1/2.71828 of its original value. Under this approximation the penetration is infinite - the projectile never actually comes to a stop although after travelling several times x_c it will be going so slow as to make no practical difference. If we know that there is some speed v_thr below which this approximation is no longer valid (such as when material strength forces equal the dynamic forces) we can get an idea of the distance the projectile will travel while hydrodynamic behavior dominates
x ≈ 2 x_c ln(v₀/v_thr).
Again, we find linear behavior in the sectional density, but the penetration increases only slowly with increasing velocity.

This hydrodynamic realm is where we find projectiles passing through any true fluid, such as bullets or arrows going through air en route to their targets. High speed bullets may initially exhibit nearly hydrodynamic behavior when passing through tissue.

Intermediate speed penetration

What about projectiles which are at speeds where both material and dynamic forces are important? Or what about when a projectile starts in the hydrodynamic regime but slows down to speeds where material strength dominates? Fortunately, there is an exact solution for this. We combine the hydrodynamic and material forces when finding the differential energy loss
dE = -[c_d A (E/m) ρ_t + Y_c A] dx.
To solve differential equations of this form, we re-write it as
dE/dx + c_d (A/m) ρ_t E = - Y_c A
exp(-c_d (A/m) ρ_t x) × d(E exp(c_d (A/m) ρ_t x))/dx = - Y_c A
d(E exp(c_d (A/m) ρ_t x))/dx = - Y_c A exp(c_d (A/m) ρ_t x)
and then integrate both sides with respect to x
E(x) = E₀ exp(-c_d (A/m) ρ_t x) - (Y_c m)/(c_d ρ_t) [1 - exp(-c_d (A/m) ρ_t x)].
The maximum range x_m of the projectile occurs when the kinetic energy is zero; E(x_m) = 0. This can be solved to find

xm =	m	ln	⌈	1 +	E0	⌉
	cd ρt A		⌊		(Yc m)/(cd ρt)	⌋.

If we define a threshold speed

½ vthr² =	Yc
	cd ρt

then this simplifes to

xm = xc	ln	⌈	1 +	v0²	⌉
		⌊		vthr²	⌋.

At high speed, for v₀ much greater than v_thr, we see that we again have the expected near exponential decay of energy and speed with distance. At low speed, we can make use of the Taylor expansion of the natural logarithm as z → 0
ln[1+z] ≈ z - z²/2 + z³/3 - …
and truncate the expansion to the lowest order to find
x_m = x_c ^v₀²⁄_vthr² = m v₀²⁄(2 A Y_c)
as before.

Strong, thin targets

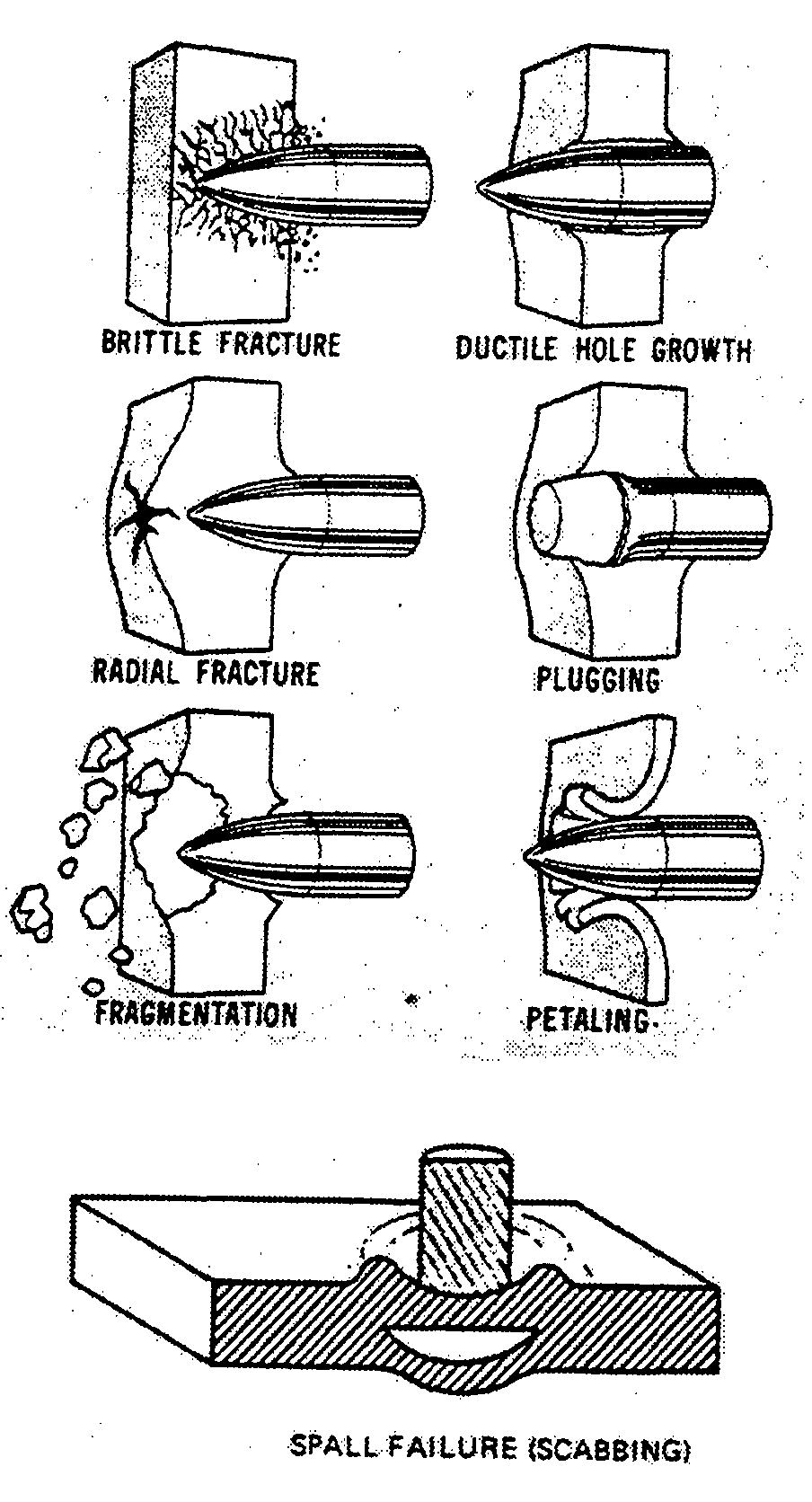
Typical penetration modes (from Army Research Laboratory report ARL-TR-1741, John F. Chinella, Brian Pothier, Martin G. H. Wells, "Processing, Mechanical Properties, and Ballistic Impact Effects of Austempered Ductile Iron," (1998))

The previous results have all assumed that the projectile is causing ductile deformation of the target, which requires compressing the target material to make room for the material in the path of the projectile to be pushed out of its way. As previously mentioned, the pressure to do so is about three times the yield strength. If the target is thin enough, however, it only needs to be pushed forward rather than compressed and pushed to the sides. This will require at most the yield strength, so it can occur at significantly lower pressures. In addition, if the target material begins to rupture, stress can be concentrated along the cracks that are formed and released by simply elongating the cracks rather than deforming the bulk material, and then bending the resulting petals out of the projectile's path or pushing aside the plug or fragments of material that break off.

Petalling

Petalling is the primary mode of penetration for thin armor. Penetration occurs in three steps. First, the initial impact of the projectile starts the portion of the plate directly in front of it moving at the same speed as the projectile. Second the impact stretches the material in front of the projectile as it makes a dent until the top of the dent ruptures. Stress in the strecthed dent is rapidly released by the formation of cracks radiating from the top of the dent, resulting in triangular petals. The third stage involves the projectile bending the petals back until they allow passage of the projectile.

1. We treat the initial acceleration of the armor plate before stretching can occur as an impulsive step. This plug of armor has a mass ½r²xρ. Momentum is conserved, so we end up with an effective mass of the projectile from this point on is
   m' = m + ½r²xρ
   and the effective initial velocity for all subsequent penetration purposes is
   v₀' = v₀ m/m'.
   Compute the new energy of the projectile plus plug as
   E₀' = ½ m' (v₀')²
   
2. The energy needed to stretch the dent to the point of rupture is given by
   E_s = ½ A x Y_y.
   where Y_y is the yield strength of the armor material.

   We now need to estimate the distance over which this occurs. Let z be the depth of the dent at any given time. Since the radius is r, the length along the stretched material from the dent center to the edge can be approximated by √(r²+z²), assuming a straight line from the edge to the center and using the Pythagorean theorem. Since the original center to edge distance is r, if the armor material can stretch a proportional amount 1+ε_y before yielding then at maximum stretch the length is r × (1+ε_y). Set this equal to √(r²+z²) and use the approximation √(r²+z²) = r × (1 + ½ z²/r²) for z much smaller than r. We find that at the point of rupture,
   z_s = r √(2ε_y).
   

   During this stage of penetration, the behavior of the armor is elastic. Elastic materials act like springs, with an energy equal to E = ½ k z², where k is the effective spring stiffness. We thus find that

   k =	π x Yy
   	2 εy

   The spring force is
   F_s = k z.
   We also add in a dynamic force due to the projectile leaving the armor moving after it punches through, including losses to creation of waves in the armor. This is similar to the drag in an infinite medium, but the thickness of the medium resisting the motion is reduced by approximately a factor x/r
   F_d = ½c_d A v² ρ_t x/r.
   For simplicity of notation, let us define
   β = c_d (A/m') ρ_t x/r.
   The solution for the energy remaining at any given stretching distance z can be found using the same general method used in the section on Intermediate speed penetration
   E(z) = E₀' exp(-β z) - [exp(-β z) - 1 + β z] k/β².

3. The petals can be considered a cantilevered beam being bent at the base with a width 2πr with a radius of curvature of approximately x over an angle of π⁄2 radians. The energy to perform this bending is
   E_b = π² r x² Y_y ⁄ 4.
   While undergoing plastic yielding, the force and torque is roughly constant. The bending occurs over a distance of r, so the force is the ratio of the energy to the distance or
   F_b = π² x² Y_y ⁄ 4.
   Again, the total force is taken as the sum of the bending force and the drag force with the solution
   E(z) = E(z_s) exp(-β (z-z_s)) - Y_y (π²x²/(4β)) [1 - exp(-β (z-z_s))]
   = E₀' exp(-β z) - [exp(-β z_s) - 1 + β z_s] exp(-β (z-z_s)) π x Y_y/(2 β² ε_y) - Y_y (π²x²/(4β)) [1 - exp(-β (z-z_s))].
   The limit of penetration comes when E(z_s + r) = 0. Since x appears in the exponents (through β) and in the prefactors, there is no analytic solution. However, solving for the root of this equation is simple using methods such as bisection.

The stretching term will be a larger contribution than the bending term for targets whose thickness is less than the projectile radius, while the quadratic term in the bending contribution becomes more important as the target becomes thicker than the target. However, the quadratic increase in energy with thickness only holds as long as the energy to cause petalling is less than the energy for ductile deformation. In this sense the quadratic term enables the smooth cross-over in energy from thin to thick plates, with the former being about 6 times easier to penetrate compared to what would be expected from ductile deformation.

The strong thin target limit is the regime in which most armor penetration occurs, whether the projectile is an arrow, a sling stone, or a pistol bullet. High speed rifle bullets may occupy a regime where ductile deformation is more important, particularly for rifle bullets made of hard materials designed to pierce armor with minimal deformation. The discarding sabot long rod penetrators fired by tanks blow right past the thin strong target regime, both because the impact is so high speed that it causes significant deformation of the projectile and because the high sectional density allows penetration to a significant fraction of the projectile's very long length compared to its radius.

Deforming projectiles

At high enough speeds, the dynamic pressure of the projectile ramming its way through the target will exceed the yield strength of the projectile and it will start to deform.

This intermediate speed regime is a reasonable description of bullets passing through tissue or ballistics gelatin.

High speed limit

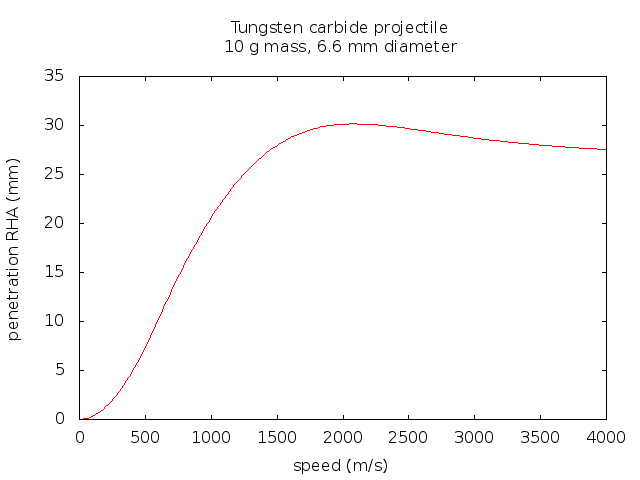
Tate model of penetration of a tungsten carbide projectile into rolled homogeneous armor. Note the initial quadratic increase in penetration with speed which rises to a maximum penetration at about 2000 m/s before falling off to the asymptotic high speed limit.

At very high speeds, the dynamic pressure of the projectile so greatly exceeds the material strength of both the projectile and the target that material strength can be neglected. As the projectile penetrates into the target, the front of the projectile is deforming and flowing away as well, jetting off to the sides and being lost. Let us consider the interface between the advancing projectile and the target, and let us also consider moving along at the speed of this interface, which we will call u. If you want, you can think of this as you sitting still while the target is rushing by in one direction at speed u, the projectile in the other direction at speed v-u, so that the interface between them is steady in front of you. At this interface, we write out the pressure balance using only hydrodynamic drag
½ ρ_t u² = ½ ρ_p (v-u)².
We can immediately see that the ratio of the rate at which the projectile is being shortened to the rate at which the target is being penetrated is given by the square root of the ratio of material densities

u	= √ (	ρp	).
v-u		ρt

So long as the projectile and target are homogeneous and in the high speed regime, this ratio holds. So, if we multiply the length of the projectile L by this ratio, we find out how far it penetrates into the target before it is all used up

xm =	L × √ (	ρp	).
		ρt

In this doubly hydrodynamic limit, the penetration is independent of the projectile speed - it doesn't matter how fast the projectile is going, it penetrates just as far! There are a few caveats to this statement - the debris is still moving with a speed of u with respect to the target, so it can still penetrate some additional distance. This is generally a small but sometimes noticable effect compared to the penetration of the original projectile. Also, the impact will forcefully throw the material of the target forward and to the sides, creating a blast wave and gouging out a crater. In some cases, the size of the crater may be much larger than the distance the projectile penetrated.

Hypervelocity impacts of meteors and orbital debris fall into this regime, as do the shaped-charge Munroe-effect jets of certain armor-piercing rounds.

Low speed limit

At low speeds, there are three possibilities

• Both the target and the projectile are fluids. In this case, the low speed limit is the same as the high speed limit.
• The pressure is enough to deform the target but not the projectile. This case has already been considered, above.
• The pressure is enough to deform the projectile but not the target. In this case the target holds steady and the projectile splashes against it. This is the realm of water balloons, and is also seen when jacketed lead pistol bullets encounter thick steel plates. Penetration is zero.

Intermediate speeds

At intermediate speeds, the material strength of either the projectile, the target, or both must be considered as well as the dynamic pressure. To this end, we add a material strength to both sides of our hydrodynamic pressure equation, denoted R_t for the target and Y_p for the projectile.
½ ρ_t u² + R_t = ½ ρ_p (v-u)² + Y_p.
The projectile is slowed down by the pressure of its deformation, but not its hydrodynamic pressure; for a projectile of length L

-ρp L	dv	= Yp.
	dt

We also know that v-u is the rate at which the projectile is becoming shorter

dL	= u-v
dt

The resulting equations have no anaytic solution and must be numerically integrated. The alorithms for performing this integration are not particularly difficult, but go beyond the simple-physics level of this document. Interested readers are directed to the following peer-reviewed journal articles

• A. Tate, "A Theory for the Deceleration of Long Rods After Impact", J. Mech. Phys. Solids, 1967, Vol. 15, pp. 387 to 399.
• A. Tate, "Further Results in the Theory of Long Rod Penetration", J. Mech. Phys. Solids, 1969, Vol. 17, pp. 141 to 150.

Thin, strong plates

What about when a squishy lead bullet smacks into a strong but thin steel plate? The intermediate speed equations work well for ductile penetration, but have serious difficulties for other failure modes. For example, they preduct zero penetration of lead bullets into steel at speeds of less than 800 m/s or so. This is accurate - if the steel is sufficiently thick. Against thick steel, lead will just splash and not even dent the steel. However, as the steel gets thinner, it takes less and less force to stretch it until at some point even lead can punch through. Anyone who has ever gone plinking against used cans knows this.

So what can we do? One estimate is to take the average non-dynamic force exerted by the plate and take this for the material strength. Using our previous model for non-deforming projectiles, we know the non-dynamic energy to penetrate is
E_nd = ½ A x Y_y + π² r x² Y_y ⁄ 4.
This energy is transfered over a distance of
z_p = r (1+√(2ε_y)).
Thus the average non-dynamic pressure is

Rav =	End	.
	zp

To account for the lessened amount of material in front of the projectile, we multiply the dynamic term for the target by x/r. This leads to a modified pressure ballance equation
½ ρ_t u² x/r + R_av = ½ ρ_p (v-u)² + Y_p.
This is then integrated in the same way as penetration at intermediate speeds against deep targets. The integration gives a penetration, and we keep varying x until the penetration equals z_p. The larger of the ductile penetration and the slab thickness penetrated by stretching to failure is used for the final penetration.

Here is a test of our method. Several bullets used by the U.S. military are listed in the table below, along with measured data on the thickness of Rolled Homgeneous Armor (RHA) penetrated and our calculated values, using R_av = 1000 MPa, R_t = 4500 MPa, ε_y = 0.121, and ρ_t = 7800 kg/m². Bullets listed as tungsten cored were assumed to have the properties of tungsten carbide: Y_p = 6000 MPa, ρ_p = 15,800 kg/m². Steel cored bullets were assumed to have Y_p = 2500 MPa, ρ_p = 7800 kg/m². Lead bullets are calculated with Y_p = 50 MPa, ρ_p = 11800 kg/m². The length of the bullet is calculated as if a constant radius given by half the caliber for the density of lead, actual radius of the core is then found by scaling the caliber by √(ρ_p / 11800 kg/m²);

Name	Caliber	Material	Bullet mass (g)	Bullet speed (m/s)	Predicted penetration (mm RHA)	Actual penetration (mm RHA)
M995	5.56×45mm NATO	WC	3.37	1013	13	12
M61	7.62×51mm NATO	steel	9.8	838	8.1	7
M993	7.62×51mm NATO	WC	8.2	910	15	15
M2 AP	.30-06	steel	10.74	810	8	13
M2 ball	.30-06	lead	9.8	840	6.8	6.8
M2	.50 BMG	steel	45.8	856	14	19
M8	.50 BMG	WC	40.34	887	26	25

The results are remarkably good, although the steel cores of many bullets may be made of a harder steel than what is assumed here, or perhaps the steel penetrator has a carbide cap.

How does all this apply to GURPS?

The received wisdom among GURPS cognoscenti is that projectile damage is equal to a proportionality factor times the square root of the kinetic energy of a projectile, while armor protection is linear in thickness. The scaling factor can be a function of projectile radius, but if so is typically increasing as a weak power of the radius (such as radius^½ or radius^1⁄₆. This can be seen to scale badly in several respects:

• Penetration will not be linear in sectional density, because the frontal area has too little of an effect.
• Penetration is linear in projectile speed, or proportional to the square root of the energy. As we have seen, this fails both at low speeds (where penetration is quadratic in speed) and at high speeds (where speed has relatively little effect on penetration). The regime where this scaling could best be justified is in the transition between strong thin targets, with a target thickness significantly less than the projectile width, and strong thick targets where the thickness is significantly more than the projectile width - a relatively narrow region of parameter space.

Of course, it is impossible to choose one value of penetration that scales correctly with projectile speed against all targets without introducing more parameters (and more on-the-fly math) into the stats of game-relevant targets than just DR and HP. However, the above model allows proper scaling with projectile and target size, and should give results that are less likely to break suspension of disbelief.

But what does this mean?

What does the GURPS damage formula above actualy represent? Clearly it is penetration by a rigid projectile, but penetration of what material? It is not Rolled Homogeneous Armor (RHA, the real-life and GURPS standard for penetration, with DR 70 = 2.54 cm of RHA), since lead bullets go sploosh when they hit steel. Lead is much softer than steel, and a thin jacket of copper is not going to chage that. A splooshing lead bullet can still penetrate RHA if it delivers enough dynamic pressure, but not as a rigid body. Since just about any armor material will be harder than lead, the same argument applies to rock, brick, titanium, boron nitride bullet resistant plates, and so on.

So what about living bodies? We know that a HP 10 character provides DR of 10, and humans are roughly 25 cm thick. Lead pistol bullets or shotgun slugs will not usually deform when punching through meat and gristle and viscera without special engineering (for example, hollow points). Rifle bullets go fast enough that simply exposing lead at the tip will cause them to deform and mushroom out, but a simple skin of copper over the tip will prevent this. Does human tissue have a v_thr of 100 m/s? Unfortunately for our inquiry, tissue has widely varying material properties, with skin responding quite differently from muscle which is different from liver tissue which is different from tendon which is different from bone. Bullets are usually tested and callibrated on a gelatin tissue simulant, which is supposed to mimic the resistance of human tissue. How well it does this is open to debate, but at least it provides consistency and uniformity. A v_thr of about 50 m/s does a reasonable job of describing penetration of various pistol and rifle bullets into ballistics gelatin. If we throw in the interaction of the bullet with bones, skin (which is much tougher and stronger than muscle tissue), cartilage, and sinew a v_thr of 100 m/s does not seem too unreasonable. All the cartridges on the table above have a bit less penetration than you would expect from ballistics gelatin tests, which we can again attribute to tougher and stronger tissues the bullet may have to punch through on its passage through its unfortunate victim.

Then what about armor penetration?

A lead bullet will not cause bulk ductile deformation of steel until it gets to a speed of more than 870 m/s or so. If the steel is thick enough, it will not even dent at speeds lower than this. The bullet just splashes off.

Of course, lead bullets can punch through thinner steel plates, as numerous street signs along rural roads can attest. If we treat the steel as a strong thin plate, we find the following values for penetration using our test projectiles using the methods described for deforming projectiles on strong, thin plates with the values for RHA as the armor material and either lead, steel, or tungsten carbide for the bullet

Cartridge	Jacketed Lead		Hardened Steel		Armor Piercing		GURPS Penetration (DR)
	Penetration (mm)	Penetration (DR)	Penetration (mm)	Penetration (DR)	Penetration (mm)	Penetration (DR)
.22 LR	1.4	3.9	3.3	9	3.8	11	5.5
9 mm Parabellum	2.2	6.1	5.1	14	6	16	9
.45 ACP	1.9	5.2	4.3	12	5	14	7
.44 Magnum	3.5	9.7	8.2	23	9.6	26	12.5
00 Buckshot	1.9	5.2	4.5	12	5.6	15	4.5
5.56×45mm NATO	5.7	16	6.4	18	14	38	17.5
7.62×51mm NATO	6.7	18	8	22	16	44	24.5
.50 BMG	12	34	14	39	29	80	42
4 mm Gauss	10	28	11	32	21	57	69
Shortbow hunting arrow			0.84	2.3			3.5/2.5
Longbow war arrow			1.8	4.7			6.5/4.5

We see that GURPS damage consistently over-estimates the penetration from lead bullets. The copper jacket will help a little, as will the fact that most bullets are made of alloys of lead with tin or antimony than harden the metal. A Y_p = 500 MPa and the usual density of lead gives good agreement with GURPS penetration values. GURPS damage gives very good results for slow moving projectiles like arrows, and an armor divisor of (2) is a good estimate for the penetration of hard, dense armor piercing bullets at speeds above 200 m/s or so.

What about extreme cases?

We have seen that our model reproduces GURPS damage reasonably well for even low energy projectiles, such as arrows. What about the other extreme? To some extent this is unimportant for most engagements with man-portable weapons, because even Ultra-Tech super-duper gauss guns have to punch through atmosphere and at super-high velocities we are firmly in the doubly hydrodynamic limit. Air has a density of 0.0012 g⁄cm³, so even a projectile made out of the densest matter held together by chemical bonds (about 20 g⁄cm³) will only travel about 130 times its own length. For man-portable weapons, this will mean ranges of only a few meters.

Of course, not all combat occurs between people mucking about in an atmospheric soup. GURPS may also deal with spacecraft duking it out with kinetic kill interceptors. These hypervelocity projectiles will penetrate about 4.5 times their length into meat and 1.6 times their length into RHA. Of more concern, however, is the way all that kinetic energy will turn into the energy of a blast wave as the impact violently pushes aside the target with the projectile splashing out into the impact debris, all expanding at supersonic speeds. As mentioned, the kinetic energy is E = ½ m v². One kg of TNT has an energy of 4.2 MJ. At high enough speeds, the armor penetration of the blast will exceed that of the projectile.

Sadly for us, the GURPS rules for explosive damage also scale badly, such that large explosions do too much damage and small explosions too little. Since we are tinkering with the rules anyway, here's how we can fix it: First, we assume the fine folks at Steve Jackson Games got the damage about right for one pound of TNT. Then we use the fact that blast damage scales with the cube of the distance (not the square of the distance, as follows from the GURPS rules). Contact damage would also be expected to scale as the cube of the explosive yield. Combining all this gives a damage in dice of 6×(8.8×M×REF)^1⁄3 for an explsoive of mass M. For a kinetic energy E in joules, it then follows that the explosive damage is 6×(2.1×E⁄1,000,000)^1⁄3.

Should this be a Linked effect to the impact, or a Follow-Up? Since a projectile that is not entirely fluid will slow down as it penetrates from the forces of impact, the dynamic pressures will be higher near the surface than after it has reached near its maximum penetration (if only by a little bit), so the distance drilled near the surface contribute more to the blast than deeper in. This argues for a Link rather than a Follow-Up.